ENIGMES MATHEMATIQUES

"la diligence et la mouche" Une diligence va de A vers B distants de 60 Km
à l'allure de 12 Km/h. Une mouche qui vole à; 20 Km/h part de B au même instant et se dirige vers A.
Quand elle rencontre la diligence elle repart vers B, à son arrivée à B, elle repart à la rencontre de la diligence... et ainsi de suite jusqu'à l'arrivée de la diligence à B. Combien de Km la mouche a-t-elle parcourus ?


Le cycliste Pour son entraînement un cycliste effectue des trajets aller-retour sur une piste pentue. Il gravit la montée à la vitesse de 15 Km/h.
A quelle vitesse doit-il effectuer le retour descente pour que sa vitesse-moyenne sur le parcours aller-retour soit de 30 Km/h ?

Les scoubidous Pour fabriquer un scoubidou, il faut 2 fils de 60 cm chacun. Le fil se vend par bobine de 2 m. Dans une classe de CM2 chacun des 28 élèves souhaite en fabriquer un. Trouver la question à ce problème mathématique. Puis chercher la réponse.

Le cube
ll y a donc 11 développements possibles, en répertoriant les assemblages contenant des lignes de 4 carrés (6), les lignes de 3 carrés (4), et 1 ligne de 2 carrés. comme support à manipuler nous avions des carrés emboîtables et formant charnière, ce matériel existe aussi sous d'autres formes géométriques.


La diligence et la mouche
Là, faire un schéma peut bloquer. Il ne faut pas se focaliser sur la rencontre mais globaliser la situation. Il est utile de passer par la question intermédiaire: Combien de temps met la diligence pour aller de A à B ? la mouche volera donc également pendant ce même temps, qui multiplié par sa vitesse nous donnera alors la distance parcourue.
Pour la mouche, malgré tous ses va et vient, le temps de vole sera égal au temps mis par la diligence pour aller de A à B.
Avec les élèves on peut utiliser le mime comme support à la compréhension, afin de mettre en évidence que la diligence fait son parcours régulièrement, que la mouche vole pendant le temps mis par la diligence pour aller de A à B.


Validation Valider une réponse mathématique, c'est s'appuyer sur un postulat, un théorème, une propriété, acceptés par tous et que l'on n'a pas besoin de démontrer, c'est une tâche essentielle en mathématiques, on ne peut se contenter de preuve visuelle ou de simple persuasion d'avoir la bonne réponse, il faut prouver et valider .
Ici Définition de la vitesse V=D/T donc D= T x V donc T= D/V
Solution Temps mis par la diligence T =D/V 60Km : 12Km/h =5h
Distance parcourue par la mouche D=VxT 20Km/h x 5h = 100Km


Le cycliste
La notion de vitesse moyenne est différente la moyenne des vitesses. La moyenne arithmétique n'a pas de sens ici et ne peut être assimilé à la vitesse moyenne.
Si l'on trouve comme réponse 45 Km/h, ce n'est pas possible. En fait pour ce problème et avec ces données il n'y a pas de solution. C'est la démonstration par l'absurde, en montrant que notre solution n'est pas possible que l'on va utiliser, la démonstration par l'algèbre est plus longue et complexe ( la consulter dans le classeur de prises de notes).
Validation on utilise encore la formule de la vitesse. V=D/T et non (Va+Vb) : 2
On peut utiliser une simulation en attribuant au parcours une distance choisie par exemple 45 Km de côte, donc pour la gravir il mettrait 45Km : 15 km/h= 3h et pour la descendre 45Km : 45 Km/h =1h donc
il mettrait 4h pour parcourir 90 Km ce qui ne peut nous donner 30 Km/h de vitesse moyenne. dans cette simulation donc sur cette distance la vitesse moyenne est de 22.5 Km/h. Sur un parcours aller retour de 120 Km elle serait de 30 Km/h.


Les scoubidous
C'est une situation que l'on peut vivre aisément et réellement en classe. Ce peut être une situation-problème à résoudre avant d'acheter le fil ,il faut penser en faisabilité et économie. Exploiter pleinement les bobines de fil avec un minimum de chutes .
Faire chercher la question permettra de délimiter le champ de validation de la réponse. "Quel est le nombre minimum de bobines que nous devrons acheter pour permettre à chacun de réaliser un scoubidous avec deux fils de 60 cm ?
Il n'est donc pas question de faire (60 cm x 2 x 28 élèves) : 2m car dans ce cas on transforme la réalité, on fait comme si le fil était vendu en longueur continue, on ignore la vente par bobine de 2m. Dans ce cas faire un schéma peut être utile.
Solution Dans une bobine 2m : 0.60m = 3 fils de 60cm + 20 cm de chute inutilisable.
Pour 28 élèves (28 x 2fils) : 3 = 18.666 encore un retour à la situation pratique puisqu'on ne peut acheter que des bobines complètes, il en faut donc 19.


Le puzzle Avec ces 4 pièces. Peut-on faire un carré ?
Peut-on faire un rectangle ?
Justifiez et validez votre réponse.

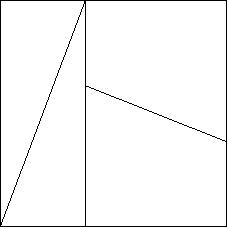
Le puzzle est à construire puis à découper et l'on essaie de former un carré, là c'est assez simple et rapide.

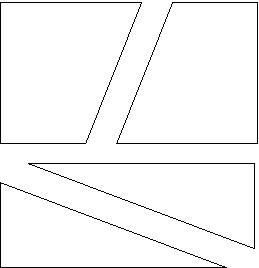
Pour le rectangle:
La première réaction est de dire j'ai trouvé, voilà ce que j'obtiens, l'écart est sûrement dû a un mauvais découpage puis si l'on valide car on ne peut se contenter de cette constatation visuelle. On se rend compte seulement après la vérification mathématique que ce n'est pas possible d'obtenir un rectangle à partir du puzzle fournit.
Validation On doit avoir des surfaces ayant la même aire, le carré initial doit avoir la même aire que le rectangle obtenu. Aire du carré initial 8 x (5+3)=64
Aire totale des pièces isolées 64
Aire du rectangle obtenu (8+5)x5=65
La différence minime est passée inaperçue, il a fallu la vérification mathématique pour s'apercevoir de l'erreur. C'est ce genre de rupture qui aide à construire le besoin de validation et de vérification d'une réponse qui nous apparaît juste de prime abord.
Il est possible de valider par les angles en prouvant par le calcul que les points de l'apparente diagonale du rectangle obtenu ne peuvent être alignés.

sur Macintosh LCIII, depuis le 20.02.1996

Site réactualisé le: 6 Mars 2002